How to Unit Test Akka.NET Actors with Akka.TestKit
An Introduction to the Akka.TestKit
In this post we introduce the Akka.TestKit module - a library that makes it easy to unit test Akka.NET actors using all of the popular .NET unit testing frameworks.
A Brief End-to-End Akka.TestKit Example
Before going deep into the TestKit, here’s an end-to-end example of what a test usually looks like.
[TestFixture] //using NUnit
public class UserIdentityActorSpecs : TestKit{
[Test]
public void UserIdentityActor_should_confirm_user_creation_success()
{
var identity = Sys.ActorOf(Props.Create(() => new UserIdentityActor()));
identity.Tell(new UserIdentityActor.CreateUserWithValidUserInfo());
var result = ExpectMsg<UserIdentityActor.OperationResult>().Successful;
Assert.True(result);
}
}
80% of your tests will be this simple: create an actor, send it a message, and expect a response back. Let’s explore how to do it.
What unit testing frameworks are support by Akka.TestKit?
The TestKit currently has support for NUnit, XUnit, XUnit2 and VSTest.
In this post we will focus on the core pieces you need to know that are shared across all of the above testing frameworks. Each framework has its own specific extensions to the core TestKit API (assertions, etc.). All code samples in this post use the NUnit package.
Now, let’s get into the nuts and bolts of testing your actors with Akka.TestKit.
Akka.TestKit Essentials
The TestActor
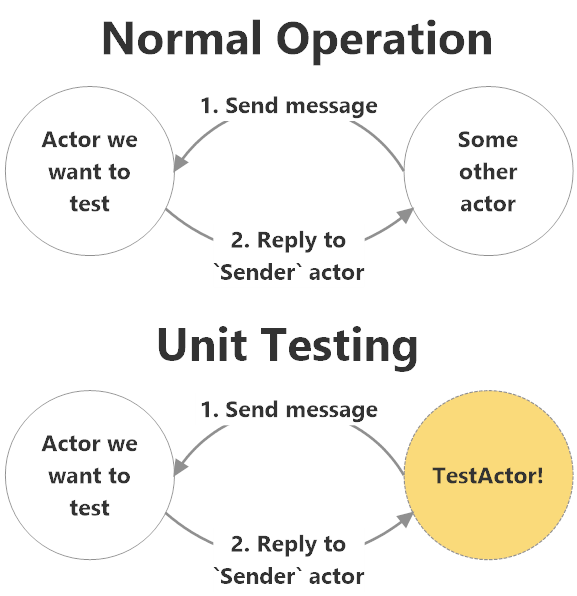
The TestActor acts as the implicit sender of all messages sent to any of your actors during unit tests. Unless you specify otherwise, the TestActor will be the Sender of all messages sent to actors in your tests.
This makes it very easy to test how actors respond to messages they are sent. Many actors reply to sender, and this reply is collected by the TestActor in an internal ConcurrentQueue.
Here’s a visual comparison of how the TestActor acts as the implicit Sender and intercepts responses back to Sender from actors in your tests:
The TestActorSystem (Sys)
This is the built in ActorSystem that used inside the TestKit. You access it by calling Sys. The Sys ActorSystem gets torn down and recreated between each individual test.
N.B. We tear down
Sysbetween each individual test method, even within a single test fixture, in order to achieve correct test isolation. That way none of the asynchronous operations that were started in a previous test can create side effects for the current test.
Inside your tests, you call Sys to instantiate actors within the TestActorSystem, like so:
// create an actor in the TestActorSystem
var actor = Sys.ActorOf(Props.Create(() => new MyActorClass()));
Create your actors within Sys so that your actors exist in the same ActorSystem as the TestActor. If you don’t, TestActor won’t be able to receive messages and your ExpectMsg calls will time out.
FYI, all actors you create in a given test won’t be alive in later tests as Sys is rebuilt for each test.
Expecting messages: ExpectMsg & ExpectNoMsg
You can use ExpectMsg to assert that the TestActor receives a message of the given type. You can also use ExpectNoMsg to assert that the TestActor receives no message.
ExpectMsg calls to a queue in the TestActor and returns the message at the head of that collection. You can store this message (or a property of the message) in a variable to perform extra assertions on it, e.g.:
ExpectMsg Example
public UserIdentityActor()
{
Receive<CreateUserWithValidUserInfo>(create =>
{
// create user here
Sender.Tell(new OperationResult() { Successful = true });
});
Receive<CreateUserWithInvalidUserInfo>(create =>
{
// fail to create user here
Sender.Tell(new OperationResult());
});
Receive<IndexUsers>(index =>
{
_log.Info("indexing users");
// index the users
});
}
// other code omitted for brevity...
// ExpectMsg will assert that a message of the specified type is received
// and return it, so you can store the result in a variable for further
// inspection and assertions
[Test]
public void Identity_actor_should_confirm_user_creation_success()
{
_identity = Sys.ActorOf(Props.Create(() => new UserIdentityActor()));
_identity.Tell(new UserIdentityActor.CreateUserWithValidUserInfo());
var result = ExpectMsg<UserIdentityActor.OperationResult>().Successful;
Assert.True(result);
}
ExpectNoMsg Example
[Test]
public void Identity_actor_should_not_respond_to_index_messages()
{
_identity.Tell(new UserIdentityActor.IndexUsers());
ExpectNoMsg();
}
Be aware that by default, ExpectMsg has a 3 second timeout. You can override this by passing a TimeSpan to it.
Ensuring work completes on time: Within
Many systems using Akka.NET have soft realtime requirements. Developers of such systems need to build time constraints into their tests. Within helps you introduce the same time constraints into your test that you have in your real system.
Within sets the max time allowed for its block to execute. You can nest Within blocks several levels deep. You can use any other assertions or TestKit features inside of a Within block.
Within() Example
public class TimeConstrainedActor : ReceiveActor
{
private ILoggingAdapter _log = Context.GetLogger();
private readonly int _delay;
public TimeConstrainedActor() : this(0) { }
public TimeConstrainedActor(int delay)
{
_delay = delay; // milliseconds
Receive<string>(s =>
{
Thread.Sleep(_delay);
Sender.Tell("ok");
});
}
}
public class TimeConstrainedActorSpecs : TestKit
{
[TestCase(100, 300)]
public void Actor_should_respond_within_max_allowable_time(int delay, int cutoff)
{
var a = Sys.ActorOf(Props.Create(() => new TimeConstrainedActor(delay)));
// sets a maximum allowable time for entire block to finish
Within(TimeSpan.FromMilliseconds(cutoff), () =>
{
a.Tell("respond to this");
ExpectMsg("ok");
});
}
}
Advanced TestKit Usage
Now we’re going to go over the advanced tools within the TestKit that you will use less often. What we’ve already covered is what you’ll use 80%+ of the time and handles almost all cases.
BlackHoleActor
The BlackHoleActor is a special-purpose actor that will not respond to anything. No matter what message you tell the BlackHoleActor, it will not respond. BlackHoleActor is perfect for testing failure conditions. Common failure conditions are when an actor or service dies, or an operation times out.
Example
Let’s assume that we have an IdentityManagerActor that creates new users. IdentityManagerActor collaborates with an AuthenticationActor to get CreateUser requests validated. If the AuthenticationActor times out, the IdentityManager should fail the CreateUserRequest.
This is easy to test: all we have to do is swap the BlackHoleActor for the AuthenticationActor. Then all requests—including CreateUser—will time out:
public IdentityManagerActor(IActorRef authenticationActor)
{
_authenticator = authenticationActor;
Receive<CreateUser>(create =>
{
var senderClosure = Sender;
// this actor needs it create user request to be authenticated
// within 2 seconds or this operation times out & cancels
// the Task returned by Ask<>
_authenticator.Ask<UserResult>(create, TimeSpan.FromSeconds(2))
.ContinueWith(tr =>
{
if (tr.IsCanceled || tr.IsFaulted)
return new UserResult(false);
return tr.Result;
}).PipeTo(senderClosure);
});
}
// other code omitted for brevity...
[Test]
public void IdentityManagerActor_should_fail_create_user_on_timeout()
{
// the BlackHoleActor will NEVER respond to any message sent to it
// which will force the CreateUser request to time out
var blackhole = Sys.ActorOf(BlackHoleActor.Props);
var identity = Sys.ActorOf(Props.Create(() => new IdentityManagerActor(blackhole)));
identity.Tell(new CreateUser());
var result = ExpectMsg<UserResult>().Successful;
Assert.False(result);
}
Repeat assertions on racy code with AwaitAssert
AwaitAssert is a assertion that polls on an interval until its assertions pass, or it times out. AwaitAssert is useful for any test where we may need to check a condition many times (e.g. a race condition). This is also good for tests where you expect a condition within a time window, but you’re not sure when exactly.
AwaitAssert Example
[TestCase(3, 2)]
[TestCase(4, 3)]
public void AuthenticationActor_should_verify_its_ready_within_max_time(int maxSeconds, int authDelaySeconds)
{
// create auth actor with 5 second delay built in
var authProps = Props.Create(() => new AuthenticationActor(TimeSpan.FromSeconds(authDelaySeconds)));
var auth = Sys.ActorOf(authProps);
// assert that not ready
auth.Tell(new CheckIfReady());
ExpectMsg(false);
// initialize the AuthenticationActor (with delay)
auth.Tell(new GetReady());
// poll every 250ms until AuthenticationActor says it's ready or we time out
AwaitAssert(() =>
{
auth.Tell(new CheckIfReady());
ExpectMsg(true);
}, TimeSpan.FromSeconds(maxSeconds), TimeSpan.FromMilliseconds(250));
}
Monitor actor termination with Watch()
Just as with your normal actor code, you can set up any actor in a test to DeathWatch another actor just by Watch()ing its IActorRef.
This is often useful to check that a certain actor is killed by application logic, to check that self-terminating actors shut down when conditions are right. Any time you need to verify that an actor shuts down in a given scenario, you can use Watch in your tests. This pair nicely with ExpectTerminated(), which expects a Terminated message for a given IActorRef.
For example:
[Test]
public void UserStatsActor_should_shut_down_when_UserSessionActor_dies()
{
// using a TestProbe as a stand-in / throwaway actor here
var user = CreateTestProbe("user");
var stats = Sys.ActorOf(Props.Create(() => new UserStatsActor(user.Ref)));
// TestActor is now watching the UserStatsActor
Watch(stats);
// kill the UserSessionActor
Sys.Stop(user);
// verify that the UserStatsActor shut itself down
ExpectTerminated(stats);
}
Test for logs, dead letters, an undeliverable messages with EventFilter
Here is a simple example of testing to see if an actor logs a certain message. The syntax is almost identical for checking DeadLetters:
[Test]
public void Identity_actor_should_log_user_indexing_operation()
{
EventFilter.Info("indexing users").ExpectOne(() =>
{
_identity.Tell(new UserIdentityActor.IndexUsers());
});
}
The EventFilter is a tool to verify that actors write certain log messages. It can also detect if messages go to DeadLetters.
By default, EventFilter matches are exact. You can also change the match criteria to check for messages containing a substring.
Accessing Internal Actor State: TestActorRef
You can use the TestActorRef to access the internal state of an actor. You get a TestActorRef by calling the ActorOfAsTestActorRef method.
Be aware that the TestActorRef is a fully synchronous actor / unit test, so it will not play well with actor types that employ additional async behavior to do their jobs (e.g. the PersistentActor & AtLeastOnceDeliveryActor from Akka.Persistence)
Using TestActorRef will allow you to read internal actor state without having to send the actor a message, which is normally not possible. It will not allow you to directly modify internal actor state, or access private fields.
How do I get a TestActorRef?
You call ActorOfAsTestActorRef.
By default, ActorOfAsTestActorRef() will create the TestActorRef as a child of Sys. There is an overload to create TestActorRef as a child of any actor you have a reference to.
When to use TestActorRef
Generally, you want to avoid using TestActorRef. Using it for general testing scenarios is NOT RECOMMENDED. Why? You want your tests to simulate the real system as much as possible. Non-test actors can’t access each others internal state. And your tests should reflect this as much as possible.
In reality, if one actor wants to know the internal state of another actor then it must send that actor a message. I recommend you follow the same pattern in your tests and don’t abuse the TestActorRef. Stick to the messaging model in your tests that you actually use in your application.
That said, the TestActorRef has its uses. Such as verifying internal actor state or the side effects of an operation. This usually comes up when you need to verify data that you won’t expose via a message contract.
TestActorRef Example
// in Blackhole.cs
[Test]
public void AuthenticationActor_should_keep_internal_count_of_users_created()
{
// In this case, we're setting up a ActorOfAsTestActorRef
// to be able to directly access the internal state of the actor.
// Generally, THIS IS NOT RECOMMENDED as you want to test the actor
// from the outside, as it will be used in reality.In real use,
// actors can't access each others internal state.
// make an AuthenticationActor that will always successfully create users
var authProps = Props.Create(() => new AuthenticationActor(true));
var auth = ActorOfAsTestActorRef<AuthenticationActor>(authProps);
// ACCESSING INTERNAL ACTOR STATE
// assert that actor will always return successful ops
Assert.True(auth.UnderlyingActor.Successful);
var identityProps = Props.Create(() => new IdentityManagerActor(auth));
var identity = Sys.ActorOf(identityProps);
// ACCESSING INTERNAL ACTOR STATE
// assert that auth user has not created any users
Assert.AreEqual(auth.UnderlyingActor.UsersCreated, 0);
// create some users
var usersToCreate = 4;
for (int i = 0; i < usersToCreate; i++)
{
identity.Tell(new CreateUser());
var result = ExpectMsg<UserResult>().Successful;
Assert.True(result);
}
// ACCESSING INTERNAL ACTOR STATE
// assert that count has been kept, and is correct
Assert.AreEqual(auth.UnderlyingActor.UsersCreated, usersToCreate);
}
The TestProbe
The TestProbe is a flexible, programmable utility player. Think of it like a more flexible and configurable TestActor. The TestProbe has the base assertions and message interception capabilities of the TestActor. But you can also program the TestProbe for whatever custom behavior you want. TestProbe can send its own messages, ignore messages that don’t match a rule, reply to the sender of the last message, and much more.
The TestProbe has all the capabilities of the TestActor and then some. As an added bonus, you can run many probes in parallel.
You can program the probe to do whatever you need it to, and use it in many locations and situations. If you don’t know how else to solve your problem, odds are good you’ll end up solving it with a TestProbe.
TestProbe Example
Here are two simple examples of using a TestProbe. First as a stand-in for another actor, and in the second example as a a more programmable TestActor.
[Test]
public void UserSessionActor_should_register_itself_with_presence_on_startup()
{
// use TestProbe as stand in for FriendsPresenceActor
var presence = CreateTestProbe("userPresence");
var userProps = Props.Create(() => new UserSessionActor(_fakeUser.Generate(), presence));
var user = Sys.ActorOf(userProps);
presence.ExpectMsgFrom<RegisterUser>(user, message => message.User.Equals(user));
}
// omitted for brevity...
[Test]
public void FriendsPresenceActor_should_alert_other_users_when_friend_comes_online()
{
var presence = ActorOfAsTestActorRef<FriendsPresenceActor>("presence");
// create probes in place of users
var user1 = CreateTestProbe("user1");
var user2 = CreateTestProbe("user2");
var user3 = CreateTestProbe("user3");
// make those probes send a message I want
user1.Send(presence, new RegisterUser(user1));
user2.Send(presence, new RegisterUser(user2));
user3.Send(presence, new RegisterUser(user3));
// pre-check we have the right number of subscribers
Assert.AreEqual(3, presence.UnderlyingActor.Subscribers.Count);
// trigger by having a probe send msg that I want
user1.Send(presence, new UserOnline(user1));
// other user probes should have been informed of new friend presence
user1.ExpectNoMsg();
user2.ExpectMsgFrom<UserOnline>(presence, online => online.User.Equals(user1));
user3.ExpectMsgFrom<UserOnline>(presence, online => online.User.Equals(user1));
}
Akka.TestKit FAQs
How do I test an actor’s lifecycle?
There are many ways to test actor lifecycle. Here are a few common approaches:
- verify that the actor calls
IDisposable.Dispose()on a dependent resource - have the actor send messages during certain lifecycle hook methods
- have the actor register itself with another actor
- have the actor change its response to a message after restarting
In this example, we verify that the actor disposes of a repository. That disposal is part of the actor shutdown process and lets us see if it actually stopped.
[Test]
public void RepositoryActor_should_dispose_repo_on_shutdown()
{
var repo = new FooRepository();
var repoActor = Sys.ActorOf(Props.Create(() => new RepositoryActor(repo)));
// assert repo has not been disposed
Assert.False(repo.Disposed);
Sys.Stop(repoActor);
Thread.Sleep(TimeSpan.FromSeconds(1));
// assert repo has now been disposed by RepositoryActor's PostStop method
Assert.True(repo.Disposed);
}
How do I test a parent/child relationship?
Testing the parent/child relationship is more complicated. This is one case where Akka.NET’s commitment to providing simple abstractions makes testing harder.
The simplest way to test this relationship is with messaging. For example, you can create a parent actor whose child messages another actor once it starts. Or you may have the parent forward a message to the child, and then the child can reply to the original sender, e.g.:
public class ChildActor : ReceiveActor
{
public ChildActor()
{
ReceiveAny(o => Sender.Tell("hello!"));
}
}
public class ParentActor : ReceiveActor
{
public ParentActor()
{
var child = Context.ActorOf(Props.Create(() => new ChildActor()));
ReceiveAny(o => child.Forward(o));
}
}
[TestFixture]
public class ParentGreeterSpecs : TestKit
{
[Test]
public void Parent_should_create_child()
{
// verify child has been created by sending parent a message
// that is forwarded to child, and which child replies to sender with
var parentProps = Props.Create(() => new ParentActor());
var parent = ActorOfAsTestActorRef<ParentActor>(parentProps, TestActor);
parent.Tell("this should be forwarded to the child");
ExpectMsg("hello!");
}
}
How do I test a SupervisorStrategy?
This is another place it’s easy to focus too much on the implementation of your code. You want to focus on testing the intended effects of your code, not testing the framework itself.
Here are a few common tests related to SupervisorStrategys:
- test that actors throw exceptions in certain conditions
- test that actors stop or restarted given bad input
- test that exceptions create side-effects such as log messages, error reports, or disposed resources
SupervisorStrategy tests tend to be more integrative and need more thinking from you. Here are two example tests:
[Test]
public void OddEvenActor_should_throw_exception_on_bad_input()
{
// create coordinator, which spins up odd/even child actors
var coordinator = Sys.ActorOf(Props.Create(() => new OddEvenCoordinatorActor()), "coordinator");
// assert we're set up right
coordinator.Tell(1);
coordinator.Tell(2);
ExpectMsg<ValidInput>();
ExpectMsg<ValidInput>();
// test
var even = ActorSelection("akka://test/user/coordinator/even").ResolveOne(TimeSpan.FromSeconds(5)).Result;
var odd = ActorSelection("akka://test/user/coordinator/odd").ResolveOne(TimeSpan.FromSeconds(5)).Result;
// expect exception
EventFilter.Exception<BadDataException>().Expect(2, () =>
{
even.Tell(1);
odd.Tell(2);
});
}
// omitted for brevity...
[Test]
public void OddEvenCoordinatorActor_should_stop_child_on_bad_data()
{
// create coordinator, which spins up odd/even child actors
var coordinator = Sys.ActorOf(Props.Create(() => new OddEvenCoordinatorActor()), "coordinator");
// assert we're set up right
coordinator.Tell(1);
coordinator.Tell(2);
ExpectMsg<ValidInput>();
ExpectMsg<ValidInput>();
// test
var even = ActorSelection("akka://test/user/coordinator/even").ResolveOne(TimeSpan.FromSeconds(5)).Result;
var odd = ActorSelection("akka://test/user/coordinator/odd").ResolveOne(TimeSpan.FromSeconds(5)).Result;
// even & odd should be killed when parent's SupervisorStrategy kicks in
Watch(even);
Watch(odd);
// we cover BadDataShutdown being sent in another test
IgnoreMessages(msg => msg is BadDataShutdown);
// even & odd should be killed when parent's SupervisorStrategy kicks in
even.Tell(1);
ExpectTerminated(even);
odd.Tell(2);
ExpectTerminated(odd);
}
How do I change the configuration of the TestActorSystem?
You pass the HOCON string to base in the constructor of your TestFixture.
In this example, I am changing the loglevel to INFO to hide DEBUG messages. But you can override / manipulate whatever config settings you need to. You can only change the config per TestFixture, not per test.
For example:
[TestFixture]
public class TestHoconActorSpecs : TestKit
{
/// <summary>
/// TestFixture with custom HOCON passed into the TestActorSystem.
/// </summary>
public TestHoconActorSpecs() : base(@"akka.loglevel = INFO") { }
// can also pass in a full HOCON string w/ nesting, e.g.
//public TestHoconActorSpecs() : base(@"
//akka {
// loglevel = INFO
//}") { }
[Test]
public void TestHoconActor_should_log_debug_messages_invisibly_when_loglevel_is_info()
{
// should see no debug messages from the actor since overrode the config
EventFilter.Debug("TestHoconActor got a message").Expect(0, () =>
{
var actor = Sys.ActorOf(Props.Create(() => new TestHoconActor()));
actor.Tell("foo");
});
}
}
How do I test scheduled messages?
A common question is this: “how do I test a message scheduled for an hour from now, without waiting for an hour?”
You can manipulate time in your tests so that you don’t have to sit around waiting. TestKit uses virtual time that you can manipulate by changing the Scheduler used. If you use the TestScheduler you can call Advance or AdvanceTo to jump forward in time.
This is the process required to manipulate time in your tests:
- Configure
Systo use theAkka.TestKit.TestSchedulerby passing in HOCON. - Cast the
Schedulerto theTestSchedulerin a property. Use this newSchedulerin your tests instead of the built-in scheduler. - When creating your actors, you must configure
Propsso your actors use theCallingThreadDispatcher. This forces the scheduler run on the same thread as the test, so thatAdvancecall works as intended. - Use
AdvanceandAdvanceToto manipulate time as needed in your tests. - Use assertions,
TestProbe,ExpectMsg, etc. as you wish.
Here’s an example:
/// <summary>
/// TestFixture with virtual time <see cref="TestScheduler"/> turned on so we can jump forward in time!
/// </summary>
public ScheduledMessageActorSpecs() : base(@"akka.scheduler.implementation = ""Akka.TestKit.TestScheduler, Akka.TestKit""") { }
/// <summary>
/// Cast the TestActorSystem scheduler to be a TestScheduler
/// </summary>
private TestScheduler Scheduler => (TestScheduler)Sys.Scheduler;
[Test]
public void ScheduledMessageActor_should_schedule_ScheduleOnceMessage_appropriately()
{
var actor = Sys.ActorOf(Props.Create(() => new FutureEchoActor()).WithDispatcher(CallingThreadDispatcher.Id));
var delay1 = TimeSpan.FromHours(1.5);
actor.Tell(new ScheduleOnceMessage(delay1, 1));
Scheduler.Advance(delay1);
var firstId = ExpectMsg<ScheduleOnceMessage>().Id;
Assert.AreEqual(1, firstId);
}
If you’re interested in learning how to design your actors and Akka.NET applications to be testable, we cover testability patterns in our Akka.NET Design Patterns training.
What use cases are you running up against in your own tests? Let us know in the comments how this helps you make your system more reliable.
If you liked this post, you can share it with your followers or follow us on Twitter!
- Read more about:
- Akka.NET
- Case Studies
- Videos
Observe and Monitor Your Akka.NET Applications with Phobos
Did you know that Phobos can automatically instrument your Akka.NET applications with OpenTelemetry?
Click here to learn more.
